Pythonで楕円フーリエ変換

2023-02-18
Image

楕円フーリエ変換の概要

物体輪郭の各ピクセル座標を複素平面に射影する。
（ $N$ 個のピクセルから構成されると仮定）

z[n]=x[n]+\mathrm{i}y[n],\\,\\, (n=0, \cdots, N-1)

輪郭線を離散フーリエ変換する。

Z[k] = \frac{1}{N} \sum_{n=0}^{N-1}z[n]\exp\{-\mathrm{i}nk\}

この変換が楕円フーリエ変換。
この和は連続空間のフーリエ積分、計算結果はフーリエ係数に対応しており、
適当な次数まで $Z[k]$ を足し上げると次数に応じた形状復元ができる。

\hat{z}[n] = \sum_{k=-K}^{K}Z[k]\exp\{\mathrm{i}kt\}

実装例

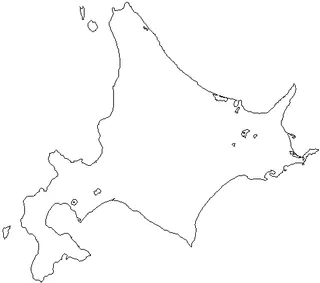
形状解析のための楕円フーリエ変換を
参考に北海道本島の輪郭を取り上げた。
CraftMAPから白地図画像をダウンロード。

実行環境

Python: 3.8.5
matplotlib: 3.4.1
numpy: 1.20.2
scikit-image: 0.18.1

from matplotlib import pyplot as plt
import numpy as np
from skimage import io
from skimage import measure

輪郭抽出

本島輪郭だけを画像から抽出する。skimage.measure を利用して画像中の輪郭面積を計算し、最大面積を探索する手法を選択した。

def find_largest_contour(image):
    """ 最大面積の輪郭をフィルターする補助関数
    Args:
        image: 画像
               （グレースケール）
    Returns:
        results: 最大面積輪郭の座標値
                 (row, column)
    """
    contours = measure.find_contours(image)
    contour_sizes = [
        len(c) for c in contours
    ]
    results = contours[
        np.argmax(contour_sizes)
    ]
    return results

hokkaido = io.imread(
      './data/hokkaido.png', as_gray=True
)
contour = find_largest_contour(hokkaido)

# 重心を原点に平行移動
zs = contour[:, 1] + (-contour[:, 0]) * 1j
zs -= np.mean(zs)

fig, ax = plt.subplots(figsize=(8, 8))
ax.plot(zs.real, zs.imag)
plt.show();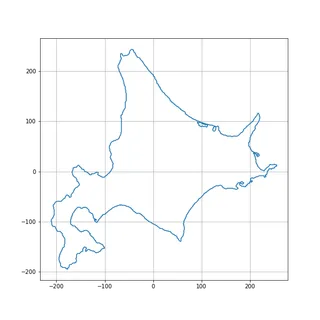

楕円フーリエ変換

numpy を使えばFFTのAPIを呼ぶだけである。

# arrayのインデックス変換・規格化
# NOTE 上式に合わせて規格化
sp = np.fft.fftshift(np.fft.fft(zs)) / len(zs)

形状復元

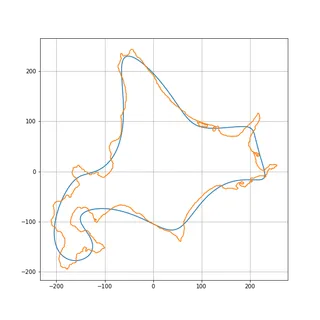
変換結果を足し合わせる。ここでは8次まで計算し粗く形状を復元する。

# ８次まで計算する
K = 8
center_sp = len(sp) // 2
cs = sp[center_sp-K:center_sp+K+1]

# フーリエ級数を計算
ts = np.linspace(
      0.0, 2.0 * np.pi, len(zs)
) - np.pi
fs = []
for t in ts:
   temp = np.array([
       cs[i] * np.exp(1j * k * t)
       for i, k in enumerate(range(-K, K+1))]
       )
   fs.append(temp.sum())
fs = np.array(fs)

fig, ax = plt.subplots(figsize=(8, 8))
ax.plot(fs.real, fs.imag)
ax.plot(zs.real, zs.imag)
ax.grid()
plt.savefig('./data/Restore.png')
plt.show();

グラフを描くと粗視化した輪郭形状を確認できる。